Les permutations
Définition :
Soit \(A\) un ensemble à \(n\) éléments (n>0).
On appelle permutation de \(A\) tout \(n\)-arrangement (rappel : \(n\)-uplet d'éléments distincts) d'éléments de \(A\).
Exemple :
Si \(A=\left\{1 ;2 ;3\right\}\), alors les permutations de \(A\) sont :
(1 ; 2 ; 3) ; (1 ; 3 ; 2) ; (2 ; 1 ; 3) ; (2 ; 3 ; 1) ; (3 ; 1 ; 2) et (3 ; 2 ; 1).
Fondamental :
Le nombre de permutations d'un ensemble non vide à \(n\geq1\) éléments est \(n!\).
Complément :
On démontre ce résultat par récurrence :
Initialisation :
Si \(n=1\), alors \(A\) est un singleton \(\left\{a\right\}\). La seule permutation est \((a)\). Or \(1!=1\) donc la propriété est initialisée.
Hérédité :
Supposons la propriété vraie pour un certain entier \(k\geq1\) donc qu'un ensemble à \(k\) éléments a \(k!\) permutations.
Démontrons qu'elle l'est pour l'entier \(k+1\), donc qu'un ensemble \(A_{k+1}\) à \(k+1\) éléments a \((k+1)!\) permutations :
Un ensemble a \(k+1\) éléments peut s'écrire sous la forme \(A_k\cup \left\{a_{k+1}\right\}\) où \(A_k=\left\{a_1 ;a_2 ;... ;a_k\right\}\) est un ensemble à \(k\) éléments.
Les permutations de \(A_{k+1}\) ont pour forme :
\((a_1 ;~~~~a_2 ;... ;a_{k+1})\), et toutes les permutation commençant par \(a_1\) : Elles sont au au nombre de \(k!\) par hypothèse de récurrence;
\((a_2 ;~~~~a_1 ;a_3 ;... ;a_{k+1})\) et toutes les permutation commençant par \(a_2\) : Elles sont au nombre de \(k!\) par hypothèse de récurrence ;
\((a_3 ;~~~~a_1 ;a_2 ;a_4 ;... ;a_{k+1})\) et toutes les permutation commençant par \(a_3\) : Elles sont au nombre de \(k!\) par hypothèse de récurrence ;
...
\((a_ {k+1};~~~~a_1 ;a_2 ;... ;a_{k})\) et toutes les permutation commençant par \(a_{k+1}\) : nombre de \(k!\) par hypothèse de récurrence.
On obtient ainsi un nombre de permutations égal à \((k+1)\times k!\) qui est égal à \((k+1)!\).
CQFD
Ainsi, la propriété est démontrée pour tout \(n\geq 1\).
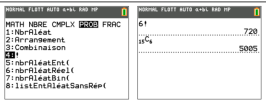
Complément : Utilisation de la calculatrice pour la factorielle :
NUMWORKS :
On utilise la touche 0 précédée de la touche alpha :
CASIO :
Touche OPTN, F6, PROB, le nombre dont ion veut la factorielle puis F1 :
TI :
Touche MATH, PRB, touche 4 :
Exemple : Le rubik's cube
Pour déterminer le nombre de "combinaisons" d'un rubik's cube, il suffit de calculer :
\(\dfrac{8!\times12!}{2} \times 3^7 \times 2^{11}\)
On pourra lire les explications ici.