Les arrangements
Définition : Factorielle
Soit \(n\) un nombre entier naturel non nul. On appelle factorielle de \(n\) le nombre entier noté \(n!\) :
\(n!=n\times (n-1)\times (n-2) \times...\times 2\times 1\).
Remarque :
Par convention, on choisit \(0!=1\).
On a \(1!=1\), \(2!=2\), \(3!=6\)...
Complément :
On peut donner une définition par récurrence de la factorielle :
\(n!=n\times (n-1)!\) et aussi \((n+1)!=(n+1)\times n!\)
Définition : Arrangements
Soient \(A\) un ensemble non vide à \(n\) éléments et \(k\) un entier inférieur ou égal à \(n\). On appelle arrangement de \(k\) éléments ou \(k\)-arrangement de \(A\) un \(k\)-uplet d'éléments distincts de \(A\).
Fondamental :
Un arrangement de \(A\) correspond à un tirage avec ordre et sans remise de \(k\) éléments de \(A\).
Nous avions vu qu'un \(k\)-uplet correspond à un tirage avec ordre et avec remise de \(k\) éléments de \(A\).
Exemple :
Si \(A=\left\{ a ;b ;c ;d ;e\right\}\), alors \((b ;a)\), \((b,c,a,e)\) sont des arrangements à 2 et 4 éléments.
Fondamental :
Soient \(n\) un entier naturel non nul, \(A\) un ensemble à \(n\) éléments et \(k\) un entier inférieur ou égal à \(n\).
Le nombre de \(k\)-arrangements d'éléments de \(A\) vaut :
\(A_n^k=n\times (n-1)\times...\times (n-k+1)\) ou encore \(\dfrac {n!}{(n-k)!}\).
Remarque :
Dans la 1re expression de \(A_n^k\), le nombre de facteurs vaut \(k\) : on peut l'obtenir en effectuant le calcul \(n-(n-k+1)+1\).
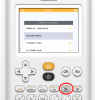
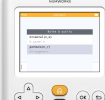
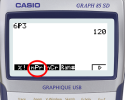
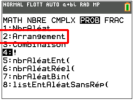
Utilisation de la calculatrice
Calcul d'un k-arrangement avec la calculatrice :
NUMWORKS :
On utilise la boîte à outils :
CASIO :
On appuie sur OPTN, puis F6, puis PROB,
Ensuite, pour calculer le nombre de 3-arrangements d'un ensemble à 6 éléments, on appuie sur 6 nPr 3 :
TI :
On appuie sur la touche MATH, puis on choisit PRB, puis 2 :nPr :
